Du 10/01 au 14/01/2022 – La Physique en PCSI

Cette semaine, les colles de Physique porteront sur le filtrage fréquentiel de signaux.

On pourra poser l’étude d’un filtre passif ou d’un filtre actif (avec Amplificateur Linéaire Intégré).

Attention, seul l’A.L.I. idéal et en régime linéaire est au programme. Les défauts de l’A.L.I. (slew rate, …) ainsi que le fonctionnement en régime saturé (comparateur à hystérésis, …) sont donc hors programme.

Le théorème de Millman est hors programme. L’obtention de la fonction de transfert d’un quadripôle avec A.L.I. doit donc se faire avec les lois des mailles et des nœuds.

La connaissance de fonctions de transfert canoniques n’est pas exigible.

Questions de cours
Compétences exigibles en exercices

Soit le circuit RLC série en régime permanent sinusoïdal forcé à la pulsation $\omega$ .
Calculer l’expression de l’amplitude $I_m$ de l’intensité dans le circuit en fonction de $E_m$ (amplitude de la tension délivrée par le générateur), $R$ , $\omega_0=\frac{1}{\sqrt{LC}}$ et $Q=\frac{1}{R}\sqrt{\frac{L}{C}}$ .
Montrer que cette amplitude est maximale pour une pulsation que l’on déterminera. Comment appelle-t-on ce phénomène ?

Soit le circuit RLC série en régime permanent sinusoïdal forcé à la pulsation $\omega$ .
• Calculer l’expression de $\tan \left(\varphi_i \right)$ , la tangente du déphasage de l’intensité dans le circuit $i(t)$ par rapport à la tension $e(t)$ délivrée par le générateur.
• Déterminer les valeurs de ce déphasage à très basses fréquences, très hautes fréquences, et à la fréquence propre. En déduire l’allure de $\varphi_i$ en fonction de $\omega$ .

Pour un phénomène de résonance, rappeler ce qu’on appelle la bande passante.
Puis, pour la cas de la résonance en intensité dans le RLC série, rappeler (sans démonstration) l’expression de la largeur de cette bande passante, en fonction de $\omega_0$ et $Q$ .

• Soit le circuit RLC série en régime permanent sinusoïdal forcé à la pulsation $\omega$ .
Calculer l’amplitude $U_{C,m}$ de la tension aux bornes du condensateur, en fonction de $E_m$ (amplitude de la tension délivrée par le GBF), $\omega_0=\frac{1}{\sqrt{LC}}$ et $Q=\frac{1}{R}\sqrt{\frac{L}{C}}$ .
• Puis rappeler rapidement (sans démonstration, pour gagner du temps) :
– La résonance a-t-elle lieu quelle que soit la valeur du facteur de qualité, comme pour la résonance en intensité ?
– Que vaut (approximativement) l’amplitude maximale à la résonance, en fonction de l’amplitude $E_m$ de la tension du générateur ?

Soit un circuit RLC série en régime permanent sinusoïdal forcé à la pulsation $\omega$ .
L’interrogateur vous donne (pour gagner du temps) l’expression de la tension complexe $\underline{u_C}$ dans le circuit, en fonction de la tension complexe $\underline{e}$ délivrée par le générateur :
$\underline{u_C}=\frac{\underline{e}}{1-\left(\frac{\omega}{\omega_0}\right)^2+\frac{j}{Q}\frac{\omega}{\omega_0}}$
en posant $\omega_0=\frac{1}{\sqrt{LC}}$ et $Q=\frac{1}{R}\sqrt{\frac{L}{C}}$ .

Déterminer le déphasage de $u_C(t)$ par rapport à $e(t)$ lorsque $\omega=\omega_0$ , lorsque $\omega \rightarrow 0$ (très basses fréquences), et lorsque $\omega \rightarrow \infty$ (très hautes fréquences).

Rappeler la décomposition en série de Fourier d’un signal quelconque $s(t)$ périodique, de période $T=\frac{2\pi}{\omega}$ .

1. Soit un signal périodique quelconque $s(t)$ . Donner la définition de sa valeur moyenne $S_{\text{moy}}=\langle s \rangle$ , et de sa valeur efficace $S_{\text{eff}}$ .
2. Que vaut la valeur efficace d’un signal sinusoïdal ?
3. Que vaut la valeur efficace d’un signal périodique quelconque en fonction de la valeur efficace de chacun de ses harmoniques ?
4. Rappeler l’expression de l’énergie stockée dans un condensateur, à l’instant $t$ . En régime permanent sinusoïdal forcé, que vaut cette énergie en moyenne au cours du temps ? Le justifier.

Sur un exemple au choix, montrer que la fonction de transfert d’un quadripôle dépend de la présence ou non d’une impédance de charge connectée en sortie.

Remarque pour les interrogateurs : nous n’avons pas encore défini la notion d’impédance d’entrée et de sortie.

Donner les définitions, pour un quadripôle :
– de la fonction de transfert $\underline{H}$ ,
– du gain $G$ ,
– du gain en décibels $G_{dB}$ .

Définir l’impédance d’entrée, et l’impédance de sortie d’un quadripôle.
Proposer un exemple.

Rappeler (sans démonstration) la condition à respecter lors d’une mise en cascade de plusieurs filtres les uns à la suite des autres, pour que la fonction de transfert (en sortie ouverte) de l’ensemble soit égale au produit des fonctions de transfert (en sorties ouvertes) de chacun.

L’interrogateur vous donne le diagramme de Bode en gain ainsi que la fonction de transfert d’un filtre passe-bas du 1^er ordre :

$\underline{H}=H_0\frac{1}{1+j\frac{\omega}{\omega_c}}$

avec ici $H_0 = 1$ . Justifier les pentes des deux asymptotes du diagramme de Bode en gain (à basses et à hautes fréquences)

L’interrogateur vous donne le diagramme de Bode en phase ainsi que la fonction de transfert d’un filtre passe-bas du 1^er ordre :

$\underline{H}=H_0\frac{1}{1+j\frac{\omega}{\omega_c}}$

avec ici $H_0 = 1$ . Justifier valeurs des asymptotes horizontales du diagramme de Bode en phase (à basses et à hautes fréquences).

L’interrogateur vous donne le diagramme de Bode en gain ainsi que la fonction de transfert d’un filtre passe-haut du 1^er ordre :

$\underline{H}=H_0\frac{j\frac{\omega}{\omega_c}}{1+j\frac{\omega}{\omega_c}}$

avec ici $H_0 = 1$ . Justifier les pentes des deux asymptotes du diagramme de Bode en gain (à basses et à hautes fréquences).

L’interrogateur vous donne le diagramme de Bode en phase ainsi que la fonction de transfert d’un filtre passe-haut du 1^er ordre :

$\underline{H}=H_0\frac{j\frac{\omega}{\omega_c}}{1+j\frac{\omega}{\omega_c}}$

avec ici $H_0 = 1$ . Justifier valeurs des asymptotes horizontales du diagramme de Bode en phase (à basses et à hautes fréquences).

L’interrogateur donne la fonction de transfert d’un filtre passe-bas du 2^nd ordre, ainsi que son diagramme de Bode en gain (les différentes couleurs correspondent à différentes valeurs du paramètre $Q$ ) :

$\underline{H}=H_0\frac{1}{1-x^2+j\frac{x}{Q}}$

où on a posé $x=\frac{\omega}{\omega_0}$ , avec ici $H_0 = 1$ .
Justifier les pentes des deux asymptotes (à basses et à hautes fréquences).
Expliquer ce qui se passe aux alentours de $x=1$ . Est-ce souhaitable pour un filtre passe-bas ? Comment choisir alors le paramètre $Q$ ?

L’interrogateur donne la fonction de transfert d’un filtre passe-haut du 2^nd ordre, ainsi que son diagramme de Bode en gain (les différentes couleurs correspondent à différentes valeurs du paramètre $Q$ ) :
$\underline{H}=H_0\frac{-x^2}{1-x^2+j\frac{x}{Q}}$

où on a posé $x=\frac{\omega}{\omega_0}$ , avec ici $H_0 = 1$ .
Justifier les pentes des deux asymptotes (à basses et à hautes fréquences).
Expliquer ce qui se passe aux alentours de $x=1$ . Est-ce souhaitable pour un filtre passe-haut ? Comment choisir alors le paramètre $Q$ ?

Remarque pour les étudiants : nous n’avons pas fait l’exemple du passe-haut du 2nd ordre en cours, mais adaptez les calculs du passe-bas (question précédente), la méthode est la même !

L’interrogateur donne la fonction de transfert et le diagramme de Bode en gain d’un filtre passe-bande du 2^nd ordre (les différentes courbes correspondent à différentes valeurs du paramètre $Q$ ) :

$\underline{H}=H_0\frac{j\frac{x}{Q}}{1-x^2+j\frac{x}{Q}}$

où on a posé $x=\frac{\omega}{\omega_0}$ , avec ici $H_0 = 1$ .
Justifier les pentes des asymptotes à basses fréquences et à hautes fréquences.
Comment choisir la valeur du paramètre $Q$ pour avoir un filtre très sélectif ?

L’interrogateur fournit :
• La fonction de transfert d’un passe-bas du 1^er ordre :
$\underline{H}=\frac{1}{1+j\frac{\omega}{\omega_c}}$
• La fonction de transfert d’un passe-haut du 1^er ordre :
$\underline{H}=\frac{j\frac{\omega}{\omega_c}}{1+j\frac{\omega}{\omega_c}}$

Indiquer (en le justifiant) quel type de filtre utiliser et dans quelles conditions pour obtenir un filtre :
– dérivateur ;
– intégrateur ;
– moyenneur.

Rappeler la définition de la « pulsation de coupure » (en utilisant le gain $G$ , puis le gain en décibels $G_{dB}$ ).

Donner la schématisation (norme européenne) d’un amplificateur linéaire intégré.
Quelles relations peut-on écrire pour un A.L.I. idéal et fonctionnant en régime linéaire ?

CHAPITRE B5 : Régime sinusoïdal forcé
– Établir et connaître l’impédance d’une résistance, d’un condensateur, d’une bobine en régime sinusoïdal forcé.
– Remplacer une association série ou parallèle de deux impédances par une impédance équivalente.
– Utiliser la méthode des complexes pour étudier le régime forcé.
– Relier l’acuité d’une résonance forte au facteur de qualité.
– Déterminer la pulsation propre et le facteur de qualité à partir de graphes expérimentaux d’amplitude et de phase
CHAPITRE B6 : Filtrage de signaux
– Savoir que l’on peut décomposer un signal périodique en une somme de fonctions sinusoïdales.
– Définir la valeur moyenne et la valeur efficace.
– Établir par le calcul la valeur efficace d’un signal sinusoïdal.
– Savoir que le carré de la valeur efficace d’un signal périodique est la somme des carrés des valeurs efficaces de ses harmoniques.
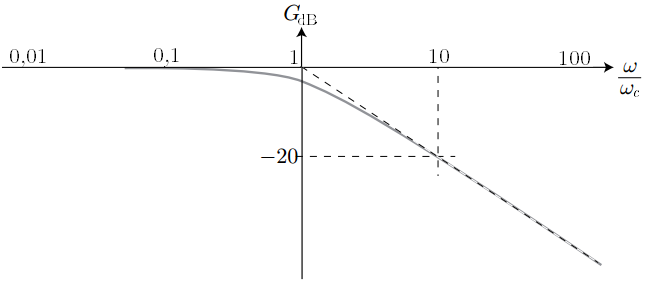
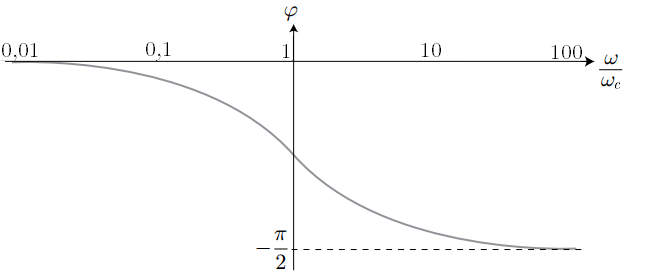
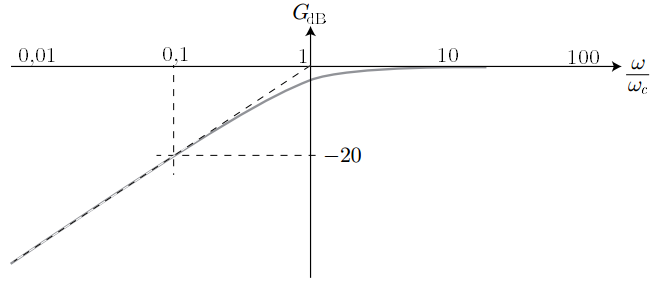
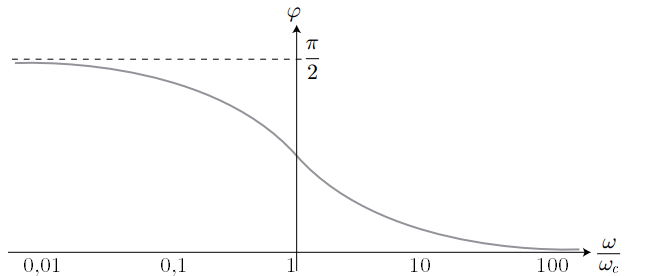
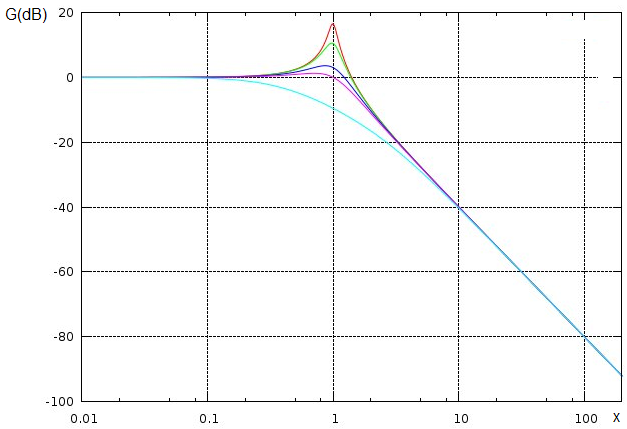
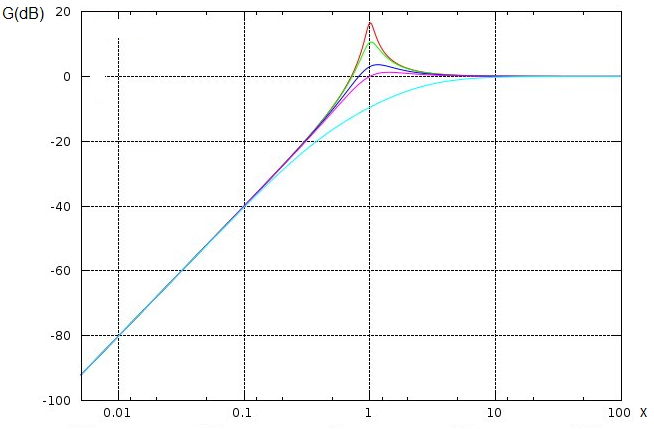
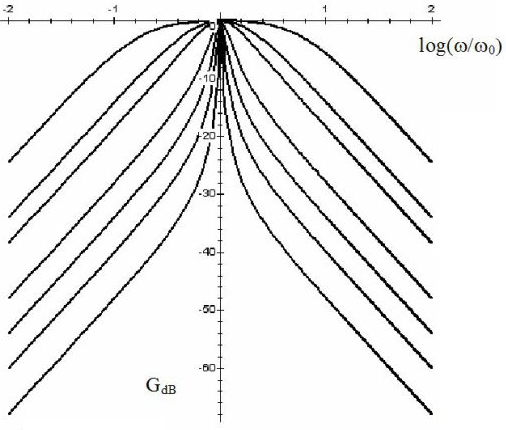
– Utiliser une fonction de transfert donnée d’ordre 1 ou 2 et ses représentations graphiques pour conduire l’étude de la réponse d’un système linéaire à une excitation sinusoïdale, à une somme finie d’excitations sinusoïdales, à un signal périodique.
– Utiliser les échelles logarithmiques et interpréter les zones rectilignes des diagrammes de Bode d’après l’expression de la fonction de transfert.
– Expliciter les conditions d’utilisation d’un filtre afin de l’utiliser comme moyenneur, intégrateur, ou dérivateur.
– Comprendre l’intérêt, pour garantir leur fonctionnement lors de mises en cascade, de réaliser des filtres de tension de faible impédance de sortie et de forte impédance d’entrée.
CHAPITRE B7 : Filtres actifs en électronique. Modèle de l’ALI idéal en régime linéaire.
– Identifier la présence d’une rétroaction sur la borne inverseuse comme un indice de fonctionnement en régime linéaire.
– Établir la relation entrée-sortie des montages non inverseur, suiveur, inverseur, intégrateur.
– Déterminer les impédances d’entrée de ces montages.

Installer comme appli sur le téléphone